KOMM-Bildungsbereich
2006—2009
»Keplers Formen«
Geometrieausstellung
Der KOMM-Bildungsbereich zeigt nach dem großen Erfolg der Ausstellung “Form und Formel” in erneuter Zusammenarbeit mit dem Bildhauer Uli Gaenshirt eine historische Geometrie-Ausstellung mit dem Titel “Keplers Formen”.
Friedrich Johannes Kepler entdeckte die Gesetze der Planetenbewegung, die nach ihm benannt wurden. Gegenstand seiner Forschung war auch die Optik.
Die Ausstellung Keplers Formen” ist Keplers geometrischen Arbeiten gewidmet. Holzschnitte und übersetzte lateinische Textpassagen aus seinen Büchern vermitteln einen direkten Blick auf diesen Teil seines Werkes. Bewegliche Objekte machen darüber hinaus die Sachverhalte auf oft überraschende Weise nachvollziehbar. Anhand von Computergrafiken wird außerdem die Relevanz seiner Ideen für die Forschung aufgezeigt. Es werden vier Themenbereiche von Keplers geometrischem Wirken in der Ausstellung behandelt.
Ellipsenkonstruktion und Kepler-Gesetz
Das erste Kepler-Gesetz besagt, dass alle Planeten die Sonne auf Ellipsenbahnen umkreisen. Um dieses Gesetz aus seinen Messergebnissen ableiten zu können, benötigte Kepler die genaue Kenntnis der Ellipsenkonstruktion.
In der Ausstellung befindet sich ein großes Wandobjekt, das mit verschiedenen Mechanismen ein und dieselbe Ellipse erzeugt.
Kepler verstand aber auch den mathematischen Zusammenhang zwischen Ellipse, Parabel und Hyperbel. Diese drei Formen können in der Lichtkegelkammer von einem rotierenden Laser an die Kammerrückwand projiziert werden.
Parkettierungen der Ebene mit regelmäßigen Vielecken
Roger Penrose, der 1973 die ersten aperiodischen Strukturen entdeckte, wurde von Keplers Zeichnungen zur Fünfeckparkettierung inspiriert.
Kristallographie und reguläre Vielflächner
Kepler führte die sechsfach symmetrische Form der Schneeflocken auf deren inneren Aufbau zurück. Die (kugelförmigen) Elementarbausteine nähmen die Platz sparendste Ordnung ein, und diese habe in einer Ebene das Muster der Bienenwaben. Die Strukturanalyse der modernen Kristallographie bestätigt die Richtigkeit seiner Gedanken.
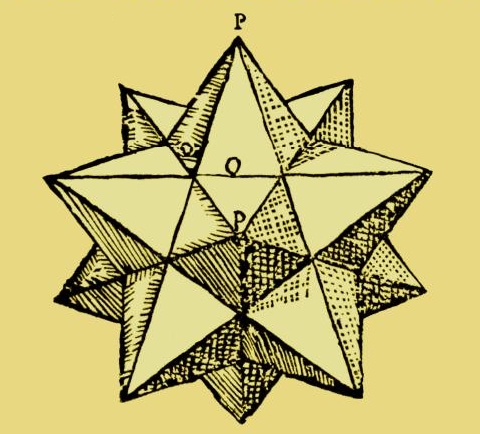
Die vier regelmäßigen Sternkörper sind nach Kepler benannt, obwohl die beiden von ihm beschriebenen Objekte zu seiner Zeit schon längst bekannt waren und die zwei anderen erst sehr viel später gefunden wurden. Kepler war jedoch der Erste, der diese und weitere reguläre Körper systematisch beschrieb.
Die Fibonacci-Reihe und der Goldene Schnitt
In der Fibonacci-Reihe ist jedes Glied die Summe der beiden vorherigen: 1,1, 2, 3, 5, 8,13, 21, 34, 55 ... Kepler konnte erklären, warum zwei sehr große, benachbarte Fibonacci-Zahlen nahezu exakt im Verhältnis des Goldenen Schnitts zueinander stehen.
(Wir danken der Université de Strasbourg, Service Commun de la Documentation, für die Erlaubnis, ihre digitalisierten Originalseiten von Keplers Büchern verwenden zu dürfen.)
Eröffnung: Do. 15.10.2009, 20:00 Uhr
Dauer: 16.10.2009—27.10.2009
täglich 10-20 Uhr, Eintritt frei
Künstlerhaus K4 im KunstKulturQuartier Nürnberg
Königstraße 93
90402 Nürnberg
1. Obergeschoss, Glasbau
Veranstalter: KOMM-Bildungsbereich
»Lange Nacht der Wissenschaften«
Samstag, den 24. Oktober 2009
Kinderprogramm:
In der Ausstellung wird gezeigt, wie sich regelmäßige Körper durch Spiegelungen hervorzaubern lassen. Außerdem erfährt man, wie man aus sechs Pappstreifen und einem Luftballon einen faszinierend schönen Fußball machen kann.
Beginn: ab 14:00 Uhr durchgehend, Altersgruppe: ab 10 Jahren
Erwachsenenprogramm:
Uli Gaenshirt, Mitglied des KOMM-Bildungsbereichs, wird die Installationen vorführen und erklären.
Beginn: ab 18:00 Uhr durchgehend
 nach oben
nach oben